支柱が強化された高エネルギー吸収型落石防護柵の防護性能に関する数値解析的検討｜建設情報クリップ

2020-07-07
特集斜面防災 | 積算資料公表価格版

支柱が強化された高エネルギー吸収型落石防護柵の防護性能に関する数値解析的検討

はじめに

我が国は，急峻な国土を有するために海岸線や山間部の道路沿いには，落石などによる被害の抑制を目的に数多くの落石防護工が設置されている。その中の一つである従来型落石防護柵（写真－1参照）は，鋼製支柱，ワイヤロープ，ひし形金網などの比較的入手しやすい材料から構成される。この防護柵は，落石対策便覧1）に基づき想定される落石エネルギーEiに対して，構成部材の塑性変形による可能吸収エネルギーの総和ETが上回るように設計される。また，その可能吸収エネルギーは柵高や柵長によって異なるものの50～100kJと比較的小さい。

一方，近年では従来型落石防護柵とは異なり，より大きな落石エネルギーに対して抵抗ができるように，ワイヤロープ端部などに緩衝装置を配置した防護柵，いわゆる高エネルギー吸収型落石防護柵が開発され，実用化されている2）～6）。同防護柵は，落石衝突時のエネルギーをワイヤロープ端部などに設置された緩衝装置によって吸収する構造であることから，一般的には非常に大きな変形を伴う。しかしながら，このように大きな変形が伴う防護柵の場合には，その変形量によっては道路空間の安全性に支障をきたす場合も報告されている。したがって，このような状況を回避するためには，落石荷重作用時における変形量を可能な限り小さくするとともに，かつ大きなエネルギーに耐え得る防護柵が要求される。

このような背景より，著者らは500kJ程度の落石エネルギーに対して，柵の変形量を2m以下とする新しいタイプの落石防護柵を開発し，その性能を実物大衝撃荷重載荷実験において検証してきた7）。一方，このような防護柵を合理的に設計するためには，実験的検討に加えて数値解析的検討は重要となる。

本研究では，同実験を対象に実験結果を適切に再現可能な解析モデルの構築を目的として，弾塑性衝撃応答解析を実施し，実験結果と比較する形で解析モデルの妥当性を検討した。さらに，構築された解析モデルを用いて，支柱間隔やスパン数を変化させた場合に関するパラメトリック解析を実施し，防護性能に与える影響について数値解析的に検討を行った。なお，本解析にはLSDYNA8）を使用した。

写真－1　従来型落石防護柵の一例

1. 実物大衝撃荷重載荷実験の概要

1.1　試験体概要

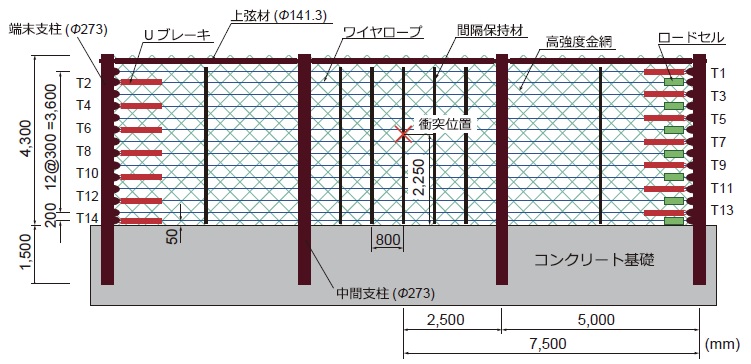
図－1には，性能照査実験に使用した落石防護柵試験体の形状寸法を示している。試験体の形状寸法（柵高×延長）は，4.0×15.0m（5m×3スパン）である。防護柵は，鋼管（外径φs＝273mm，板厚ts＝9.25mm）の内部にH形鋼（HE160M）を配置した鋼製支柱の他，それらをつなぐ上弦材，落石を捕捉するためのワイヤロープと高強度金網（以後，金網），およびロープ間の落石すり抜けを阻止するための間隔保持材から構成される。ワイヤロープにはφ18（EN 12385-4：6×36WS+IWRC，保証破断強度：204kN）を，金網には素線径4.0mmを用いている。ワイヤロープは，図－1に示すように上から300mm間隔で13本，最下端のみ200mm間隔で1本の計14本を水平に配置している。

写真－2には，試験体の各部材および全景を示している。写真－2（a）に示す上弦材は，外径φu＝141.3mm，板厚tu＝9.53mmの鋼管を使用し，支柱に取り付けられたプレート（tp＝25mm）と高力ボルトを介して接続されている。ワイヤロープ，間隔保持材および金網の結合には，写真－2（b）に示すUボルトおよび結合コイルを使用している。ワイヤロープ端部には，写真－2（c）に示すようにシャックルを介してロードセルあるいはUブレーキに接続し，さらに端末支柱に接続されている。ロードセルは図－1に示すようにロープ端部の片側のみに，Uブレーキは全てのロープ端部に設置した。なお，Uブレーキは鋼板の曲げ変形を利用した衝撃緩衝装置であり，重錘衝突時に発生するロープ張力の緩和とエネルギー吸収を目的に設置した。支柱基部はコンクリート基礎に埋め込まれている（写真－2参照）。ワイヤロープには，自重によるたわみを防ぐために初期張力を導入している。なお，初期張力はロープによって若干異なる（最小：1.2kN，最大：8.3kN）が，その平均値および標準偏差は，それぞれ6.1kN，2.15kNであった。

図－1　落石防護柵試験体の形状寸法

写真－2　試験体の各部材と全景

1.2　実験方法と測定項目

写真－3には，衝撃荷重載荷実験装置を示している。実験は，EOTA規格9）に準拠したコンクリート製多面体重錘（外寸960mm，質量1,499kg）を速度26.2m/sでスパン中央の高さ2.25mに衝突させることで実施した。実験時における実測衝突エネルギーは513kJであった。なお，実験はスイス連邦のDTC（Dynamic Test Center）10）で実施した。

測定項目は，1）重錘に内蔵されたセンサーによる加速度，2）ワイヤロープ端部に設置したロードセルによるロープ張力，高速度カメラによる3）重錘の水平変位（重錘貫入量），4）支柱天端の2方向変位，および5）実験終了後におけるUブレーキの制動距離（すべり量）である。なお，重錘内には三軸加速度センサと三軸回転速度センサの2種類が内蔵されている。写真－4には，重錘最大貫入時における防護柵の変形状況を示している。

写真－3　実験装置と重錘衝突時の状況

写真－4　重錘最大貫入時とその捕捉状況

2. 衝撃応答解析の概要

2.1　有限要素モデル

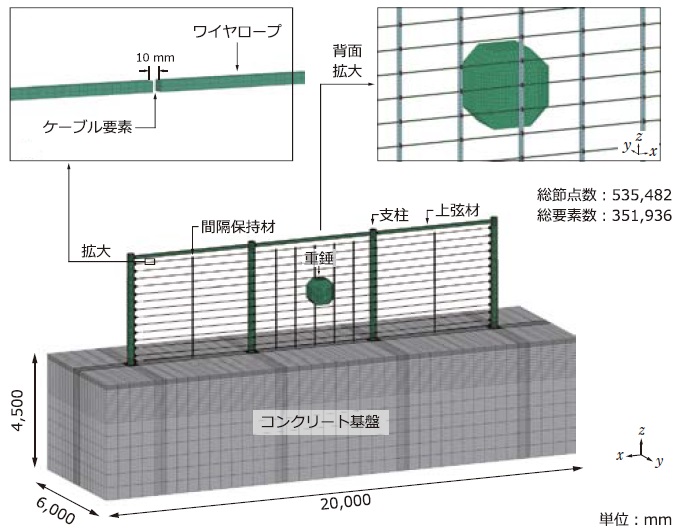
図－2には，本数値解析で用いた有限要素モデルの要素分割状況を示している。上弦材と支柱間の接続プレートには4節点シェル要素を，Uブレーキには2節点バネ要素を，それ以外の要素には8節点固体要素を用いた。総節点数及び総要素数はそれぞれ約530,000，約350,000である。なお，ワイヤロープに関しては，重錘と間隔保持材間や近接部材同士の接触判定を適切に評価するために，2節点梁（ケーブル）要素ではなく8節点固体要素を使用している。しかしながら，この場合には要素に曲げ応力が作用し，引張力のみを伝達するワイヤロープの特性と異なることになる。この問題を回避するために，ここでは，図－2に示すように8節点固体要素間に圧縮力を伝達しないケーブル要素を用いることとし，Uボルトや間隔保持材との接触を避けるように500mm間隔で配置した。ケーブル要素はワイヤロープと同じ断面とした。なお，本解析では，1）防護柵の変形性状やロープ張力に着目すること，2）重錘を間隔保持材に衝突させていること，3）実験で重錘のすり抜けが起きていないこと等から，煩雑さを避けるため，金網のモデル化は省略した。

境界条件は，コンクリート基礎底面を完全固定とし，基礎側面および正面の法線方向を固定した。また，実構造と同一条件となるように，重錘と間隔保持材および近接する部材間には，接触・剥離を伴う接触面を定義した。なお，摩擦係数は零と設定した。衝撃荷重は重錘要素をスパン中央の高さ2.25mの位置に試験体に接する形で配置し，実験条件と同等になるように重錘要素に初速度26.2m/sを付加することで作用させた。なお，本数値解析において減衰および重力は考慮していない。

図－2　有限要素モデル

2.2　材料構成則

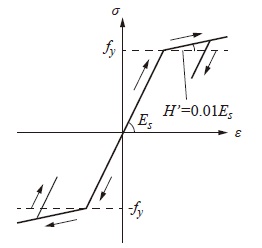
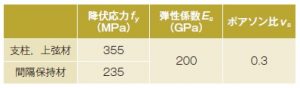
図－3には，本数値解析で用いた鋼部材（鋼製支柱，上弦材，間隔保持材）の応力－ひずみ関係を示している。ここでは，降伏後の塑性硬化を考慮したバイリニア型の等方硬化則モデルを適用することとし，塑性硬化係数H ’は弾性係数の1%と仮定した。また，各構成部材の降伏応力fy，弾性係数Es，ポアソン比νs は，表－1に示す公称値を用いた。なお，いずれの場合も降伏判定はvonMisesの降伏条件に従うものとした。

図－3　鋼材の応力－ひずみ関係

表－1　鋼材の材料物性値

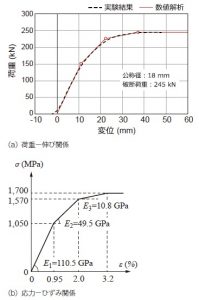
ワイヤロープに関しては，別途実施した引張試験結果を参考に応力－ひずみ関係を決定した。図－4（a）には，引張試験から得られたワイヤロープの荷重－伸び関係を示している。実験では，載荷初期にワイヤロープ特有の非線形性（素線同士の隙間の影響が主たる要因）が確認されるが，実験ではワイヤロープに初期張力を導入して設置していることから，載荷初期の非線形性を除去した赤線で示すマルチリニア型にモデル化した。本数値解析では，上記のように設定した荷重－伸び関係を用い，ロープ断面積および定着長を考慮して，図－4（b）に示す応力－ひずみ関係に変換し与えている。なお，前述のようにワイヤロープに関しては，接触判定を精度よく行うために，固体要素を用いてモデル化しているが，その一部に引張力のみ伝達するケーブル要素を一定間隔で配置することにより，変形に伴う曲げ成分を除去することとした。

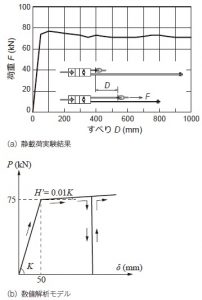
図－5には，Uブレーキ（ばね要素）に用いた荷重－すべり関係を示している。ここでは，図－5（a）に示す静載荷実験結果を参考にすべり荷重を75kNとし，すべり発生後の摩擦抵抗を簡易にモデル化するために初期勾配の1%で荷重が増加するものと仮定した。なお，実験に用いたUブレーキと同様に最大すべり量δは1,000mmと設定した。また，実際のU ブレーキは一度すべりが発生すると，除荷時においても変位は戻らず残留変位が生じる。ここでは，その現象を数値解析的に再現するために，除荷時には変位が戻らず圧縮力を伝達しないモデルを用いた。

その他のコンクリート基盤や重錘に関しては，実験終了後に大きな塑性変形が確認されなかったことから，弾性体（弾性係数Ec＝20GPa，ポアソンνc＝0.167）と仮定した。なお，コンクリート重錘の単位体積質量ρcは，実際の重錘質量と等価となるように解析モデルの体積で除すことによって与えることとした。

図－4　ワイヤロープの荷重－伸び関係および応力－ひずみ関係

図－5　Uブレーキの荷重－すべり関係

3. 実験結果と数値解析結果の比較

3.1　重錘の水平方向速度と貫入量

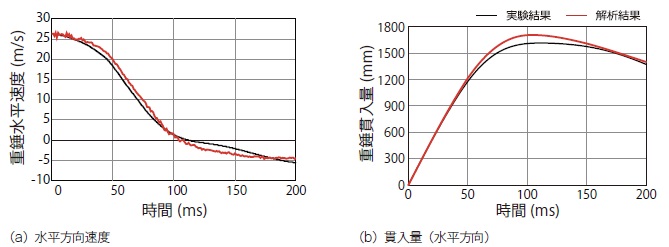
図－6には，重錘の水平方向速度および貫入量（水平方向）の時刻歴応答波形について実験結果と数値解析結果を比較して示している。なお，時間軸は重錘が防護柵に衝突した時刻を基準としている。

（a）図に示す水平方向速度を見ると，重錘衝突直後からリバウンド状態に至るまで，解析結果は実験結果を概ね適切に再現していることが分かる。

（b）図の貫入量に着目すると，数値解析結果は実験結果の立ち上がりをほぼ適切に再現しているものの，最大貫入量は実験結果よりも100mm程度大きな値を示していることが分かる。しかしながら，リバウンド状態に至る時刻は実験結果とほぼ同一であり，実験結果の応答性状を概ね再現可能であるものと推察される。

最大貫入量において若干の差異が生じる要因は，1）接触面における摩擦係数を零としていること，および2）重力や減衰を無視していることなどに起因しているものと推察される。

図－6　重錘の水平方向速度および貫入量（水平方向）に関する時刻歴応答波形の比較

3.2　ロープ張力

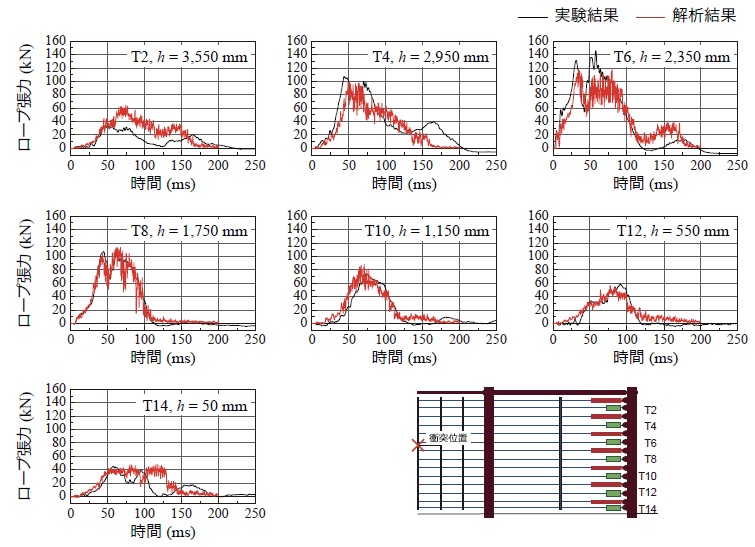
図－7には，各ワイヤロープに作用する張力の時刻歴応答波形について，実験結果と数値解析結果を比較して示している。

図より，重錘衝突位置から離れているT2やT14を除いて，数値解析結果は高周波成分が多く含まれるものの，実験結果の張力の立ち上がりや最大値，作用継続時間，最大値後の波形性状をほぼ適切に再現できていることが分かる。なお，重錘衝突位置近傍のT6に関しては，数値解析結果の張力は実験結果よりも20kN程度小さく評価されている。これは，本解析ではU ブレーキの降伏すべり荷重を75kNと設定しているのに対し，実験では動的作用によってすべり荷重が設定値と必ずしも一致しないことによるものと考えられる。

図－7　ロープ張力に関する時刻歴応答波形の比較

3.3　支柱天端の2方向変位

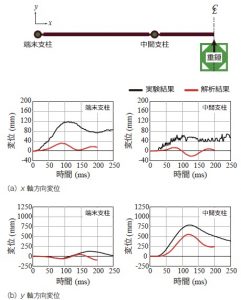
図－8には，中間および端末支柱天端の2方向（x，y軸方向）変位に関する時刻歴応答波形について，実験結果と数値解析結果を比較して示している。なお，実験結果は，防護柵直上に設置した高速度カメラの映像（写真－5）から算出している。

図－8（a）図より，x軸方向変位の実験結果を見ると，重錘衝突後に端末支柱および中間支柱のいずれも内側に変形することが分かる。なお，その変形量は端末支柱の方が大きい。一方，数値解析では，端末支柱の変形傾向は定性的に再現できているものの最大値を過小評価している。また，中間支柱に関しては100ms以降において実験結果と反対方向に変位が生じている。これは，1）実構造では支柱と上弦材は専用プレートを介して高力ボルトで接続されているのに対し，本解析ではシェル要素を用いて簡易にモデル化していること，2）試験体設置時の施工誤差などにより，その形状が必ずしも解析モデルと一致していないこと，および3）支柱と基礎地盤の節点を完全結合していること，などによるものと推察される。

次に，y軸方向変位の実験結果（図－8（b）図参照）を見ると，中間支柱は重錘衝突後に後方に大きく変形しているのに対し，端末支柱は逆に前方に若干変形していることが分かる。数値解析結果に着目すると，中間支柱の最大変位は，その発生時刻が実験結果とほぼ同時刻であるものの，実験結果が約790mmであるのに対し，数値解析結果では約552mmとなっており，その誤差は約30%である。しかしながら，波形の立ち上がりや最大変位到達後の挙動など，その傾向は実験結果と類似の傾向を示すことが確認される。

図－8　支柱天端変位に関する時刻歴応答波形の比較

写真－5　2方向変位算出のための高速度カメラ画像例（t＝
52ms）

3.4　重錘衝突後の変形状況と応力分布性状

図－9には，試験体側面の変形状況について，1）ロープ張力の実測最大時（t≒80ms），2）数値解析結果における最大重錘貫入量時（t≒105ms），3）中間支柱の最大変位時（t≒120ms）について，実験結果と数値解析結果を比較して示している。なお，数値解析結果は，重錘の状態が分かるようにスパン中央で切断して示している。図より，数値解析結果は最大張力発生時から中間柱最大変位時に至るまで，端末および中間支柱の変形性状や重錘の傾きなどを概ね再現可能であることが分かる。

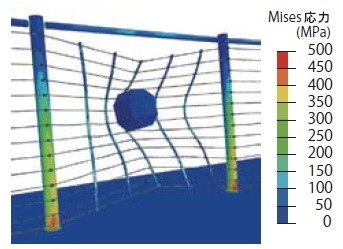
図－10には，数値解析結果の中間支柱最大変形時（t＝120ms）における中央スパン部のMises応力分布を示している。図より，中間支柱基部には降伏応力（fy＝355MPa）を超える応力が発生していることが確認される。なお，実験終了後における中間支柱は，平均で約7°傾斜しており，柱基部は塑性化しているものと判断される。

図－9　重錘衝突後における防護柵の変形状況の比較

図－10　Mises応力コンター図（t＝120ms）

4. 支柱間隔等を変化させた場合の動的応答特性に関する検討

4.1　解析モデルと解析条件

前章まででは，新たに開発した落石防護柵の防護性能について，実物大衝撃載荷実験を対象に弾塑性衝撃応答解析を実施し，解析手法の妥当性を実験結果と比較検討した。その結果，提案の解析モデルを用いることにより，実験結果のロープ張力や重錘貫入量をほぼ適切に再現可能であることが確認された。以上より，本章では，支柱間隔やスパン数が異なる場合の動的応答特性について，前節の有限要素モデルを修正する形で三次元弾塑性衝撃応答解析を実施した。

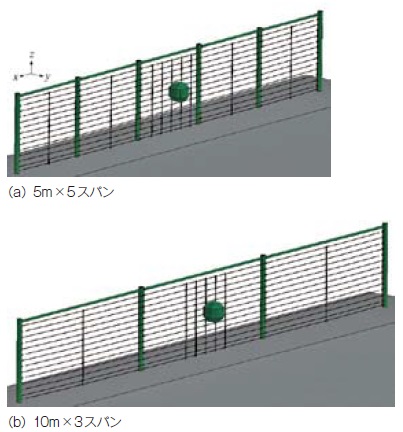
ここでは，図－11に示すように1）スパン数を3から5スパンに変化させた5m×5スパン（柵長：25m），2）支柱間隔を5mから10mに変化させた10m×3スパン（柵長：30m）の防護柵を対象に数値解析的な検討を行った。なお，柵高は4mと実物大実験と同一とした。また，構成部材の材料構成則，境界条件，重錘の質量と速度および衝突位置に関しても前節と同様の条件とした。

図－11　有限要素モデル

4.2　数値解析結果および考察

（1）重錘貫入量
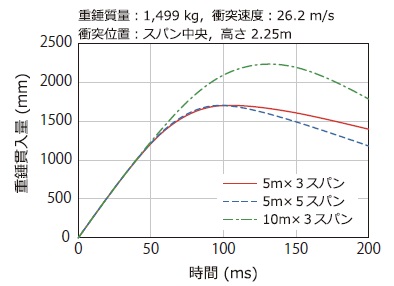
図－12には，重錘貫入量（水平方向）の時刻歴応答波形について，3ケースの数値解析結果を比較して示している。図より，5m×3スパンと5m×5スパンの数値解析結果を比較すると，最大貫入量に到達するまでの応答性状はほぼ等しいことが分かる。これより，支柱間隔を同一としてスパン数を変化させる場合には，類似の捕捉性能を有するものと考えられる。

一方，10m×3スパンの数値解析結果に着目すると，最大重錘貫入量は2,234mmを示しており，支柱間隔が5mの場合の最大変形量（1,703mm）と比較して，貫入量は1.3 倍程度大きい。したがって，支柱間隔を2倍の10mとする場合には，最大変形量が2.0mを超えることから，防護柵の最大変形量を抑えるためには支柱間隔を狭くする必要があるものと考えられる。

図－12　重錘貫入量に関する時刻歴応答波形の比較

（2）ロープ張力
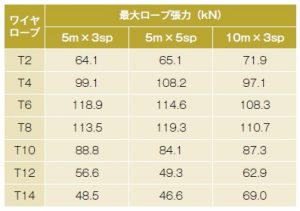
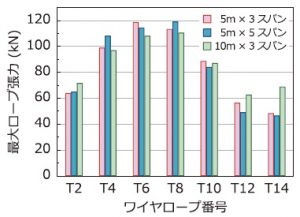
表－2には，数値解析結果より得られた最大ロープ張力を一覧にして示している。ここでは，実験時にロードセルが設置された7本のワイヤロープの結果を比較して示している。また，図－13には，それらの値をグラフ化したものを示す。

表および図より，5m×3スパンと5m×5スパンの結果を比較すると，各ロープにおいて若干の差異が確認されるものの，全体的に見るとほぼ同様な値を示していることが分かる。これは，前述の重錘貫入量波形が両者で類似の応答特性を示していることからも理解できる。

また，支柱間隔を2倍とした10m×3スパンについても，衝突部から離れているT12およびT14を除き，支柱間隔が5mの場合と顕著な差は確認されない。これは，ワイヤロープ端部に設置した緩衝構造（Uブレーキ）が機能を発揮することによって，支柱間隔にかかわらずロープに作用する最大張力がほぼ等しくなることを示唆している。なお，いずれの解析においてもU ブレーキのすべり量は最大でも607mm以下であり，限界すべり量（1,000mm）以下であることを確認している。

表－2　最大ロープ張力の比較

図－13　最大ロープ張力の比較

5. まとめ

本研究では，著者らによって開発された支柱強化型小変形防護柵の防護性能を評価するために実施した実物大衝撃荷重載荷実験を対象に，弾塑性衝撃応答解析を実施した。数値解析結果を実験結果と比較することによって，解析モデルの妥当性を検討した上で，支柱間隔やスパン数を変化させたパラメトリック解析を実施し，防護性能に与える影響について数値解析的に検討を行った。本研究の範囲内で得られた知見をまとめると，以下の通りである。

1）提案の材料構成則および解析手法を用いることによって，実験結果の重錘貫入量をほぼ適切に再現可能である。また，ワイヤロープ張力の立ち上がりや最大値，作用継続時間を大略再現可能である。

2）支柱間隔が同一でスパン数を3から5スパンに変更させた場合においても，その動的応答特性は類似の傾向を示す。

3）一方，スパン数が同一で支柱間隔を大きくする場合には，支柱間隔が小さい場合と比較して，最大重錘貫入量が大きくなる傾向が見られるものの，最大ロープ張力に関しては支柱間隔の影響は小さい。

参考文献
1）日本道路協会：落石対策便覧，2017.

2）園田佳巨，畑芳宏，福永一基：SPH 法を改良したワイヤリング防護柵の衝撃応答解析，構造工学論文集，Vol. 57A，pp. 1155-1162，2011.

3）園田佳巨，福永一基：実規模実験と数値解析によるワイヤリング落石防護柵の性能照査，構造工学論文集，Vol. 64A，pp. 811-818，2018.

4）西田陽一，石井太一，桝谷浩：ワイヤネット式落石防護柵の性能評価に関する実規模実験と解析について，第11 回構造物の衝撃問題に関するシンポジウム論文集，土木学会，CD-ROM，2014.

5） Gentilini，C.，Ubertini，F.，Govoni，L.，Gottardi，G,and Miranda，S.: Modelling of falling rock protectionbarriers，International Journal of Physical Modelling inGeotechnics，11（4），pp. 126-137，2011.

6） Koo，R. C. H.，Kwan，J. S. H.，Lam，C. et al.: Dynamicresponse of flexible rockfall barriers underdifferentloading geometries，Landslides，14（3），p p .905-916，2017.

7）石川芳治，酒井啓介，奥田峻，小室雅人：小変形バリアの機能と特徴，平成30年度砂防学会研究発表会概要集，pp. 75-76，2018.

8） Hallquist，J. O.: LS-DYNA User’s Manual，LivermoreSoftware Technology Corporation，2018.

9） EOTA，Guideline for European Technical ApprovalofFalling Rock Protection Kit（s ETAG 027），2008

10） DTC Dynamic Test Center AG（ https://www.dtcag.ch/）